The Sidewinder Sleeps Tonite
Introduction:
Slitherlink is a type of logic puzzle made popular by Nikoli, the same Japanese puzzle company that has made Sudoku popular the world over. Like most good logic puzzles, it has a set of very basic rules that can nonetheless result in devilishly difficult (and delightful!) puzzling experiences.
The rules of Slitherlink are as follows:
- A Slitherlink board is made up of a lattice of dots; in this problem, it will be a regular rectangular lattice.
- Some of the boxes (or cells) defined by the lattice have numbers within them; with a regular rectangular lattice, the numbers will be between 0 and 3 inclusive.
- The goal of a Slitherlink puzzle is to connect adjacent dots (horizontally or vertically, like the sides of boxes) so that there is a single loop that never crosses itself, with no line segments that are not part of the loop (no "dangling" segments or other, separate loops) such that every cell that has a number has exactly that many sides as segments of the loop.

|
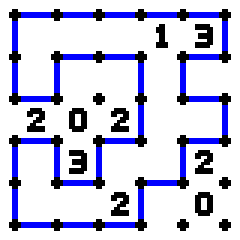
|
| Unsolved 5x5 Puzzle | Solved 5x5 Puzzle |
Given a supposedly solved Slitherlink puzzle, your task will be to determine whether or not it is indeed legitimately solved.
Input:
Input to this problem will begin with a line containing a single integer N (1 ≤ N ≤ 100) indicating the number of data sets. Each data set consists of the following components:
- A line containing two integers H, W (1 ≤ H,W ≤ 20) representing the height and width of the Slitherlink puzzle by the number of cells (not dots!) per edge;
- A series of 2H + 1 lines representing the Slitherlink puzzle, using
the following non-whitespace characters:
- 0, 1, 2, 3, ?: The numbers written inside a given cell. A ? represents an empty cell, as in the example graphic above.
- #: A dot in the lattice.
- -, |: A horizontal or vertical line segment.
- .: An empty adjacency between two dots in the lattice.
Output:
For each data set, print "VALID" if the solution is a valid solution to the given Slitherlink, or "INVALID" if the solution is not valid.
Sample Input:
2 5 5 #-#-#-#-#-# |?.?.?.1.3| #.#-#-#.#-# |?|?.?|?|?. #-#.#.#.#-# .2.0.2|?.?| #-#.#-#.#-# |?|3|?.?|2. #.#-#.#-#.# |?.?.2|?.0. #-#-#-#.#.# 5 5 #-#-#-#-#-# |?|?.?.1.3| #.#-#-#.#-# |?|?.?|?|?. #-#.#.#.#-# .2.0.2|?.?| #-#.#-#.#-# |?|3|?.?|2. #.#-#.#-#.# |?.?.2|?.0. #-#-#-#-#.#
Sample Output:
VALID INVALID